The book, “Difference Equations and Fractals” offers a captivating journey through the world of difference equations and the fascinating realm of fractals.
The book is organized into six chapters, each focusing on different aspects of this intriguing field. In Chapter 1 we offer the stability analysis of one-dimensional systems, two-dimensional systems, and various types of linear difference equations.
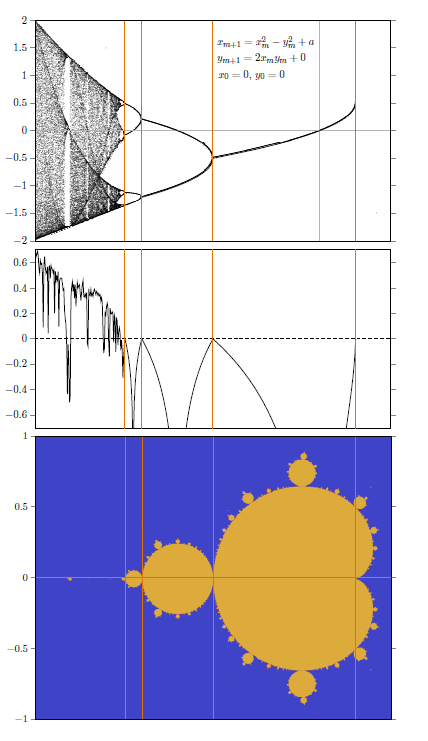
Chapter 2 delves into one-dimensional difference equations such as the logistic equation.  We also explore Feigenbaum constants, chaos, starting points, and other interesting difference equations.
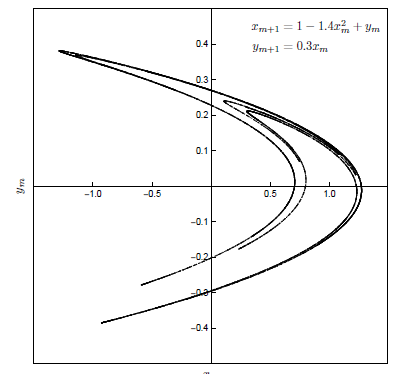
In Chapter 3 we shift our focus to two-dimensional difference equations. We analyse the Lotka-Volterra model, the modified Lotka-Volterra model, and the Hénon map. We examine concepts like Lyapunov exponents, orbits, fixed points, and limit cycles.
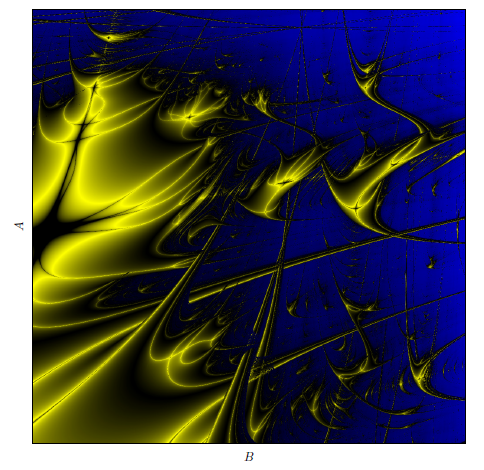
Chapter 4 takes us into the captivating world of Lyapunov images. We explore images of dynamical systems, Markus-Lyapunov images, and specifically investigate the Lyapunov image for the Hénon map. We also delve into basins of attraction and the z^2 + c map, along with analytical solutions and the number of period n solutions.
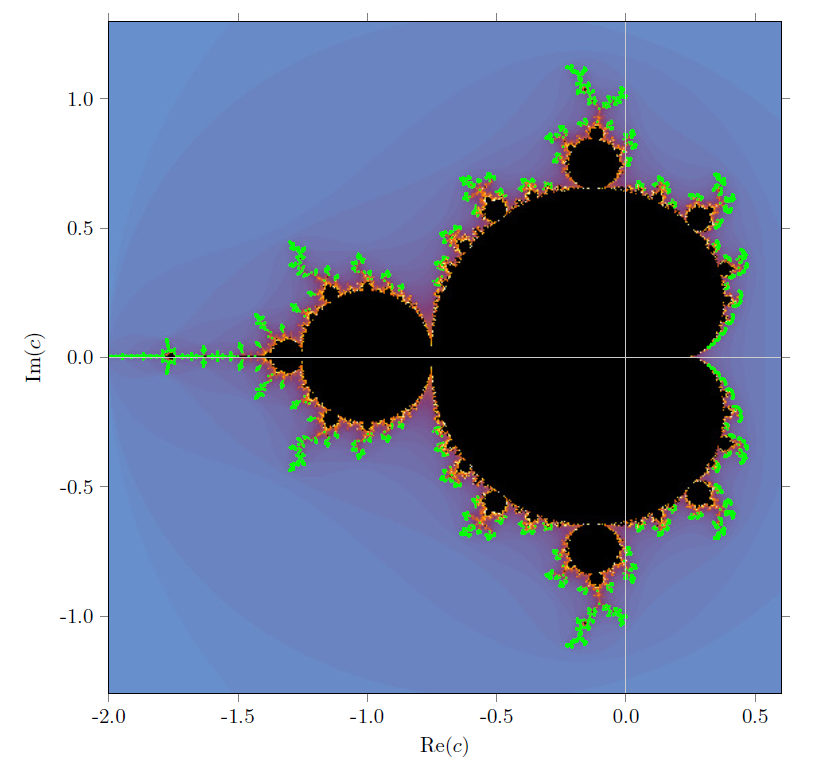
In Chapter 5, we embark on a mesmerizing journey into the realm of fractals. We explore the Koch snowflake, designing fractals, two-dimensional fractals, fractal dimension, Julia fractals, and the iconic Mandelbrot fractal.
Lastly, in Chapter 6, we delve into the intriguing topic of Misiurewicz points. We specifically focus on Misiurewicz points for the z^2 + c map.
At the end of the book, you will find appendices containing additional mathematical subjects such as a proof of a series solution, binomial identities, and Hénon eigenvalue inequality.
“Difference Equations and Fractals” serves as a comprehensive resource for those seeking a deeper understanding of the connections between difference equations and fractals..

Open the pdf and read it for free.